Эконометрика - Приложение

Приложение. ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ И МАТРИЧНОГО АНАЛИЗА

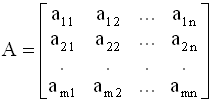
П.1. Основные определения

Прямоугольная таблица

элементы которой a_ij (i=1,2,…,m; j=1,2,…,n) - действительные или комплексные числа, называется матрицей размерности (m x n). Первый индекс у элемента a_ij обозначает номер строки, в которой находится этот элемент, второй - номер столбца. Матрицу, состоящую из одной строки, называют вектор - строкой; матрицу, состоящую из одного столбца, называют вектор - столбцом.

Матрица, у которой строки равны столбцам матрицы A, а столбцы равны строкам матрицы A, называется транспонированной относительно A. Транспонированная матрица обозначается A^T и имеет вид

Как видим, транспонированная матрица имеет размерность (n x m). Заметим, что в транспонированной матрице первый индекс ее элемента означает номер столбца, второй - номер строки. Транспонирование вектор - строки дает вектор - столбец и наоборот. Если m = n, то матрица A называется квадратной. Если выполнено равенство A^T = A, то матрица A называется симметричной. Очевидно, что симметричной может быть только квадратная матрица. Квадратная матрица A называется диагональной, если все ее элементы a_ij= 0 при , (i=1,2,…,m; j=1,2,…,n). Диагональная матрица A называется единичной, если все ее элементы a_ii= 1 (i=1,2,…,n). Сумма элементов главной диагонали матрицы A называется следом матрицы A и обозначается как tr{A}. Таким образом, след матрицы равен