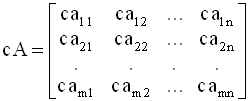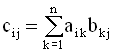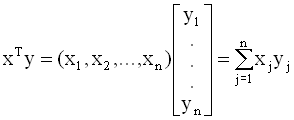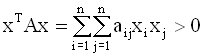П.2. Матричная алгебра

Для любой матрицы A

Две матрицы A и B одинаковой размерности равны тогда и только тогда, когда равны все их соответствующие элементы.

Суммой (разностью) двух матриц A и B одинаковой размерности называется матрица C = A + B (C = A - B), элементы которой c_ij равны сумме (разности) соответствующих элементов матриц A и B, то есть

Для произвольных матриц A, B, C одинаковой размерности имеем

Умножение матрицы A на скаляр c:

При этом имеют место следующие правила:

Произведением матриц A размерности (m x n) и B размерности (n x p) является матрица C = AB размерности (n x p), элементы которой определяются по формуле

где i=1,2,…,n; j=1,2,…,p.

Таким образом,

здесь суммирование ведется по индексу k = 1, 2,…,n.

При перемножении двух матриц A и B, количество столбцов матрицы A должно быть равно количеству строк матрицы B.

Умножение матриц:

ассоциативно

дистрибутивно

но некоммутативно, то есть в общем случае

Умножение на скаляр и транспонирование произведения матриц:

Кроме того, имеют место соотношения:

здесь c и d - скаляры.

Скалярное произведение векторов определяется следующим образом. Пусть x = (x₁, x₂,...,x_n)^T и  y = (y₁, y₂,...,y_n)^T - векторы (напомним, что под вектором мы понимаем вектор - столбец) одинаковой размерности. Скалярным произведением векторов x и y будет произведение вектор - строки x^T на вектор - столбец y, то есть

Очевидно, x^Ty = y^Tx .

Необходимо помнить, что при матричном умножении:

Квадратная матрица A называется положительно определенной, если для любого вектора квадратичная форма

Квадратная матрица A называется положительно полуопределенной, если для любого вектора

Матрица A называется вырожденной, если существует вектор , такой что Ax = 0 или A^Tx = 0.

Говорят, что прямоугольная матрица размерности m x n имеет ранг r , если она содержит r линейно - независимых строк или столбцов, записывают так: rank{A} = r.

Говорят, что матрица A - полного ранга, если rank{A} = r = m, при или rank{A} = n, при , или, что то же самое, если rank{A}=min(m,n).

Имеют место следующие соотношения:

Матрица полного ранга является невырожденной. Положительно определенная матрица имеет полный ранг. Определитель вырожденной матрицы равен нулю.

Матрица A^-1 называется обратной по отношению к невырожденной квадратной матрице , если одновременно выполнены равенства

где I - единичная матрица. Невырожденность матрицы A является необходимым и достаточным условием существования обратной матрицы A^-1. Если матрица A - диагональная, с элементами главной диагонали , то обратная матрица A^-1 будет диагональной, с элементами главной диагонали, равными .

Имеют место следующие соотношения:

Если матрица A - симметричная, то A^-1 - тоже симметричная.

Лемма об обращении матриц. Если матрицы A и C - симметричные невырожденные, то

Транспонируя последнее равенство, получим также, что

Производя здесь замены вида , , , можно получить еще одну группу подобных равенств.

Если квадратная матрица A - вырождена, то ее обратная матрица не определена.

Матрица A называется идемпотентной, если

Ранг идемпотентной матрицы A равен ее следу, то есть rank{A} = tr{A}.

Матрица A называется ортогональной, если

Очевидно, для ортогональной матрицы имеем A^-1 = A^T. Единичная матрица I является идемпотентной и ортогональной.

---

назад

предыдущая глава

приложение

оглавление

список литературы

вперед

---

Томский государственный университет - 2003