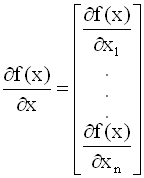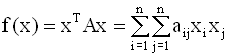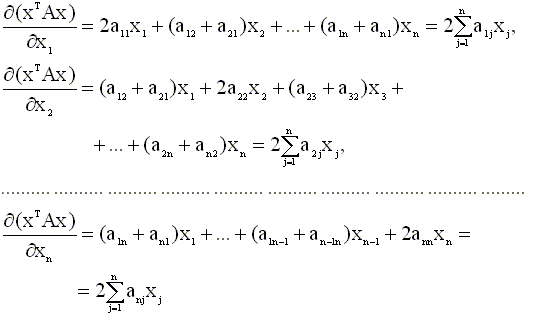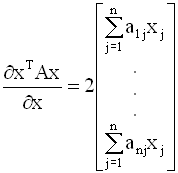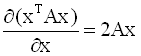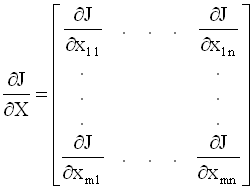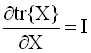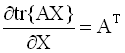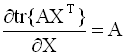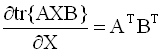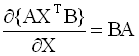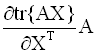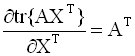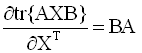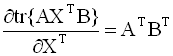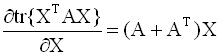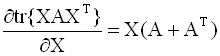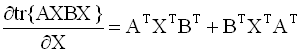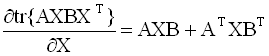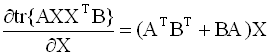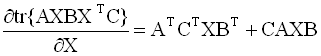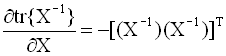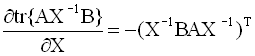П.3. Матричный анализ
Производная скалярной
функции f(x) = f(x1, x2,...,xn)
по векторному аргументу x = (x1,
x2,...,xn)определяется как
вектор - столбец частных производных
Вектор - столбец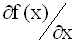 
называется градиентом
функции f.
Рассмотрим градиент
квадратичной формы
где A - симметричная
матрица. Частные производные этой
функции равны
Учитывая полученные
выражения для частных производных,
запишем выражение для градиента
или в матричной записи
Аналогично можно определить
градиент скалярной функции,
аргументом которой является матрица.
Градиент скалярной функции J(X) по
матричному аргументу X - это
матрица, которая определяется в виде
Функция J=tr{X} - след
матрицы, является функцией матричного
аргумента и можно определить ее
градиент. Формулы для вычисления
производных следа по матричному
аргументу приводятся ниже (в
предположении, что след существует):
В приведенных формулах
предполагается, что размерности всех
матриц согласованы и существуют
необходимые обратные матрицы.
