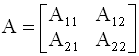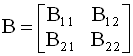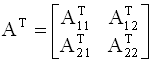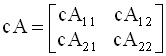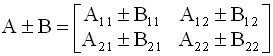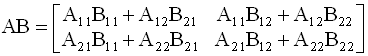|
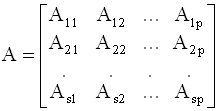
П.4. Правила действий с блочными матрицами Матрицы, элементы которых сами являются матрицами (блоками элементов), называются блочными матрицами. В общем случае блочную матрицу A можно представить в виде
где Aij - блоки (подматрицы) матрицы A. При разбиении матрицы на блоки необходимо соблюдать следующие правила: блоки Aij, (j=1,2,…,p), стоящие в i- ой "блочной строке" матрицы A должны иметь равное количество строк; блоки Aij, (i=1,2,…,s), матрицы A, стоящие в j - ом "блочном столбце" матрицы A должны иметь равное количество столбцов. При соблюдении этих правил действия с блочными матрицами аналогичны действиям с обычными матрицами, при этом роль элементов блочной матрицы выполняют ее блоки. Естественно, что при сложении (вычитании) и умножении двух (или нескольких) блочных матриц, размерности складываемых (вычитаемых) или перемножаемых блоков матриц должны быть согласованы. Пусть матрицы A и B представлены в блочном виде:
Тогда транспонированная матрица
умножение на скаляр
сумма (разность) матриц
произведение
Если блоки A11 и A22 квадратной матрицы сами являются квадратными матрицами, то
|