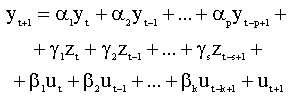Эконометрика

Глава 6. АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ

6.3. Расширенный метод наименьших квадратов: оценивание параметров модели авторегрессии - скользящего среднего с лаговыми экзогенными переменными

Ранее (см. п. 5.4.4) остался открытым вопрос оценивания параметров моделей авторегрессии - скользящего среднего. Рассмотрим один из возможных подходов к решению этой задачи с использованием рекуррентного метода наименьших квадратов. Пусть модель описывается следующим разностным уравнением

(6.26)

где, как и ранее, u_t - независимые случайные величины.

Модель (6.26) содержит как авторегрессию и скользящее среднее, так и запаздывающие (лаговые) экзогенные переменные z.

Необходимо оценить вектор параметров модели ( 6.26)

Определим вектор регрессоров

Тогда уравнение (6.26) можно записать в виде

(6.27)

Модель (6.27) не является линейной по параметрам, поскольку для того, чтобы определить прошлые значения u по прошлым наблюдениям y и z, необходимо знать истинное значение вектора параметров . Именно поэтому мы указали на зависимость вектора регрессоров от параметров. Если известна оценка вектора к моменту времени t, то можно аппроксимировать вектором , который не зависит от

Тогда модель (6.27) можно аппроксимировать моделью

(6.28)

где вектор регрессоров

остатки модели .

Модель вида (6.28) называется псевдолинейной регрессией.

Все величины, необходимые для вычисления вектора регрессоров к моменту t известны, так что оценка на шаге t + 1 может быть вычислена с использованием рекуррентного метода наименьших квадратов.

Изложенная процедура оценивания называется расширенным методом наименьших квадратов (расширенным среднеквадратичным оценивателем).