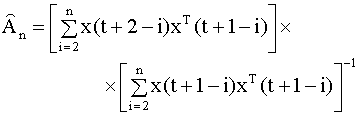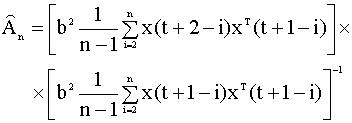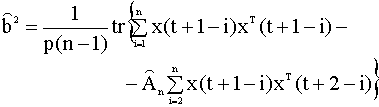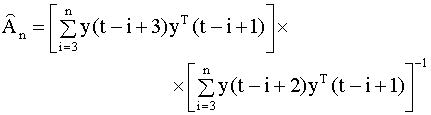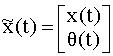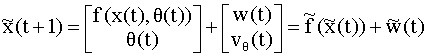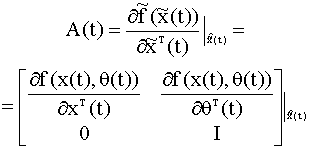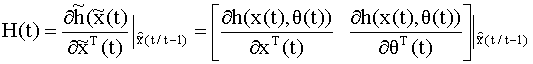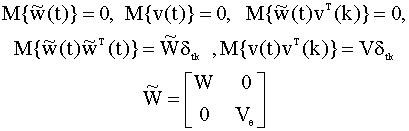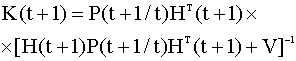|
6.6. Идентификация многомерных моделей 6.6.1. Оценивание параметров линейных моделей Оценивание параметров полностью наблюдаемых многомерных процессов Рассмотрим сначала задачу оценивания параметров многомерного процесса, описываемого векторным уравнением
где b - некоторый скалярный параметр, компоненты вектора u(t) имеют одинаковые дисперсии, равные единице. Очевидно, параметр b играет роль среднеквадратичных отклонений компонент вектора возмущений u, которые предполагаются постоянными и одинаковыми для всех компонент. Предположим, что вектор состояния x(t) полностью наблюдается (то есть доступны наблюдению без ошибок все его компоненты). Необходимо оценить p2 элементов матрицы A и параметр b. Это можно сделать, если имеется достаточно большая выборка прошлых наблюдений вектора x(t). Пусть к некоторому моменту
времени t имеется ряд наблюдений
Уравнение (6.60) можно записать в виде
Оценки вида (6.61) обладают следующим свойством: если
процесс, описываемый моделью (6.59), является
стационарным, то последовательность
оценок где Для того, что бы процесс (6.59) был стационарным, необходимо и достаточно, чтобы все собственные числа матрицы A по абсолютной величине были строго меньше единицы. Несмещенная оценка параметра b2 вычисляется по формуле
Замечание Оценки вида (6.61) и (6.62) являются оптимальными в смысле минимума дисперсий ошибок оценок. Если компоненты вектора возмущений распределены по нормальному закону, то эти оценки совпадают с оценками, полученными по критерию максимума функции правдоподобия. Оценивание параметров неполностью наблюдаемых многомерных процессов Применение фильтра Калмана в
общем случае требует знания матриц
модели А, B, H и ковариационной
матрицы шумов наблюдений V.
Ковариационную матрицу ошибок Рассмотрим один из эффективных и важных для практики подходов к оцениванию матрицы A в случае, если все компоненты вектора состояний доступны наблюдению, но с ошибками, то есть процесс описывается уравнениями
В качестве оценки матрицы A
по совокупности прошлых наблюдений
Оценки вида (6.65) обладают следующими важными свойствами: 1) Если
процесс (6.63)
стационарный, последовательность
оценок вида (6.65)
при 2)
Фильтр Калмана, построенный для
оценивания состояния процесса (6.63) по
наблюдениям (6.64),
с использованием вместо матрицы A
ее оценок (6.65),
дает оценку состояния процесса (6.63),
сходящуюся с вероятностью единица (при
Таким образом, и параметры, и состояния оцениваются одновременно. 6.6.2. Расширенный фильтр Калмана: одновременное оценивание состояний и параметров в нелинейных моделях Один из эффективных и широко используемых на практике подходов к оцениванию параметров и состояний многомерных процессов состоит в следующем. Рассмотрим нелинейную модель, описывающую нелинейный процесс
где Введем расширенный вектор состояния
и предположим, что параметры меняются в соответствии с уравнением где вектор
Уравнение наблюдений примет вид
Разложим функцию где
и заменим функцию где матрица
Таким образом, нелинейные уравнения состояния и наблюдения (6.68), (6.69) аппроксимируются линейными уравнениями вида
Поскольку эта аппроксимация
линейна относительно расширенного
вектора состояний
здесь При реализации расширенного фильтра Калмана на каждой итерации необходимо провести следующие вычисления. 1) Определить прогноз расширенного вектора состояний на один шаг. Для этого можно использовать нелинейное уравнение
вместо его линеаризованной аппроксимации. 2). Вычислить параметры фильтра на основе линеаризованной модели по следующим формулам
3). Определить оценку вектора состояний по формуле
Заметим, что в уравнении для
оценки (6.76)
используется функция Фильтр, описываемый уравнениями (6.72) - (6.76), называется расширенным или линеаризованным фильтром Калмана. Расширенный фильтр Калмана позволяет получить оценки вектора состояний расширенной системы, который включает оценки параметров, то есть параметры и состояния оцениваются одновременно. Фильтр Калмана и его различные модификации (например, только что рассмотренный расширенный фильтр) широко используются на практике в самых разнообразных областях приложений. На базе теории калмановской фильтрации созданы системы навигации и управления космическими аппаратами и другими подвижными объектами, системы управления производственными процессами и др. В настоящее время эта теория находит также широкое применение и для решения разнообразных задач в экономике и финансах. Популярность фильтра Калмана обусловлена простотой его практической реализации и возможностью эффективного решения разнообразных задач оценивания. Однако существуют проблемы, касающиеся численной реализации фильтра Калмана, основная из которых связана с возможной расходимостью фильтра. Анализу алгоритмов фильтрации на базе фильтра Калмана, его многочисленным модификациям и обобщениям, применениям в различных сферах, в том числе и в экономике, посвящено огромное количество публикаций в научных журналах, а также монографий и учебников. Мы же рассмотрели лишь некоторые вопросы, касающиеся теории калмановской фильтрации и ее применения в эконометрике.
|