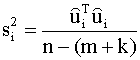Эконометрика

В.В. Домбровский - Эконометрика

Глава 7. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ

7.5. Оценка двухшаговым МНК статистических характеристик модели. Анализ адекватности

Прогноз эндогенной переменной (регрессанда) по отдельному структурному уравнению

Прогноз эндогенной переменной определяется по следующему структурному уравнению, оцененному двухшаговым МНК:

где используются наблюдаемые значения , а не их оценки, полученные на первом шаге двухшагового МНК.

Вектор погрешностей

Вектор погрешностей (остатков) в i - ом уравнении равен

(7.33)

Здесь также используются наблюдаемые значения Y, а не их регрессионные оценки. Вектор остатков (7.33) необходим при расчете оценок дисперсии случайной составляющей в отдельном уравнении, коэффициента детерминации, а также при построении тестов на автокорреляцию и гетероскедастичность.

Оценка дисперсии случайной составляющей

Оценку дисперсии случайной составляющей в i - ом структурном уравнении можно вычислить по формуле

Оценка ковариационной матрицы ошибок оценок коэффициентов структурного уравнения

Ковариационная матрица ошибок оценок структурных коэффициентов i - го уравнения модели при достаточно большом числе наблюдений n (то есть асимптотически) может быть оценена следующим образом

(7.34)

Ковариационная матрица (7.34) (ее диагональные элементы - дисперсии оценок) используется при построении t - и F - тестов и при определении доверительных интервалов и интервальных прогнозов. Все эти процедуры выполняются так же, как в случае классической многомерной регрессии и поэтому повторять их описание мы здесь не будем.

Коэффициент детерминации

При вычислении коэффициента детерминации, относящегося к i - му структурному уравнению, необходимо использовать остатки, вычисленные по формуле (7.33). Соответствующая формула имеет вид

(7.35)

Обратим внимание, что коэффициент детерминации, вычисленный по формуле (7.35) отличается от обычного коэффициента детерминации множественной регрессии, который относится к уравнению регрессии (7.31) с возмущениями , а не к уравнению (7.28). Для коэффициента детерминации справедливо неравенство

Таким образом, коэффициент детерминации может принимать и отрицательные значения (напомним, что в классических регрессионных моделях этот коэффициент принимает только неотрицательные значения). Отрицательное значение может получиться, если сумма квадратов остатков (числитель выражения (7.35)) будет больше суммы квадратов отклонений наблюдений от выборочного среднего (знаменатель выражения (7.35)).

Степень адекватности модели при оценке двухшаговым МНК считается тем больше, чем ближе коэффициент детерминации к единице.