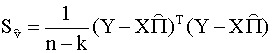Эконометрика

Глава 7. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ

7.6. Точечный и интервальный прогноз эндогенных переменных на основе приведенной формы

Точечный прогноз

Ранее мы уже упоминали о том, что приведенная форма модели может служить основой для прогноза эндогенных переменных. Процедура построения точечного прогноза состоит в следующем. Сначала определяются оценки коэффициентов матрицы П приведенной формы по формулам, используемым на первом шаге двухшагового МНК. Уравнение (7.30) дает МНК - оценку i - ой строки матрицы П или, что тоже самое, i - го столбца матрицы . Следовательно,. Используя (7.30), можно записать

(7.36)

где Y - матрица измеренных значений эндогенных переменных, . Транспонируя обе части уравнения (7.36), получим формулу для оценивания матрицы П:

Точечный прогноз вектора эндогенных переменных по значениям предопределенных переменных, измеренных до момента времени n, на шагов вперед, определяется по формуле

(7.37)

где - заданные значения предопределенных переменных в момент .

Покажем, что прогноз вида (7.37) обладает свойством несмещенности. Истинное значение вектора эндогенных переменных в момент равно

(7.38)

Используя (7.37) и (7.38), запишем уравнение для ошибки прогноза

откуда, учитывая, что , получим

Оценка получена обычным МНК при выполнении предпосылок множественной линейной регрессии, следовательно, эта оценка несмещенная, то есть и .

Замечание 1.

Ошибка прогноза зависит от числа наблюдений n, поскольку от этого зависит точность оценки матрицы .

Замечание 2.

Для оценивания матрицы коэффициентов приведенной формы можно использовать многомерную версию рекуррентного метода наименьших квадратов, рассмотренную в п. 6.4.

Интервальный прогноз

Для получения интервального прогноза эндогенных переменных (построения доверительных интервалов прогнозных значений компонент вектора ) необходимо уметь оценивать ковариационную матрицу вектора ошибок прогноза

Оценка этой матрицы вычисляется по формуле (подробный вывод см. С.А. Айвазян, В.С. Мхитарян [1]):

где - несмещенная оценка ковариационной матрицы остатков приведенной формы ,

Процедуры построения доверительных интервалов основаны на использовании F- распределения и требуют предположения о нормальном распределении случайной составляющей структурной, а следовательно, и приведенной форм модели. Мы рассмотрим два вида доверительных интервалов: доверительные интервалы (интервальный прогноз) для каждой отдельно взятой эндогенной переменной и совместные доверительные интервалы для совокупности эндогенных переменных.

Доверительный интервал для прогноза одной отдельно взятой эндогенной переменной

Доверительный интервал для прогноза отдельной эндогенной переменной при уровне доверия определяется неравенствами

(7.39)

(7.40)

где - табличное значение F - распределения для соответствующего уровня доверия и заданных степеней свободы m и n - k - m + 1, s_ii - i - ый диагональный элемент матрицы . Левая часть неравенства (7.39) задает нижнюю границу интервала, правая часть неравенства (7.40) задает верхнюю границу интервала. Это означает, что истинное значение прогноза покрывается этим интервалом со случайными границами с вероятностью .

Доверительные интервалы для совокупности прогнозных значений эндогенных переменных

Доверительные интервалы (интервальный прогноз) для совокупности эндогенных переменных задаются системой неравенств со случайными границами, которые выполняются (с заданной вероятностью) одновременно для всех истинных прогнозных значений , i=1,2,…,m. Эта система имеет вид

(7.41)

где

Замечание.

Можно показать, что ширина доверительного интервала, построенного для отдельной переменной, будет меньше, чем ширина интервала для этой переменной в совместной системе интервалов (7.41).