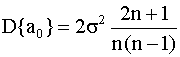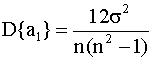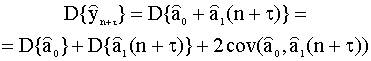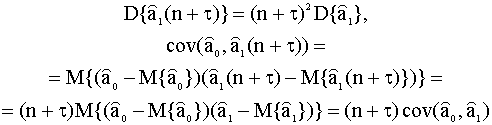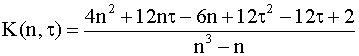|
В.В.
Домбровский - Эконометрика
Глава 8. АНАЛИЗ И ПРОГНОЗИРОВАНИЕ КОРОТКИХ ВРЕМЕННЫХ РЯДОВ С ПРИВЛЕЧЕНИЕМ ЭКСПЕРТНОЙ ИНФОРМАЦИИ Данная глава посвящена изложению некоторых доступных для студентов - экономистов методов анализа коротких временных рядов. Подробно обсуждаются проблемы, связанные с анализом временных рядов в условиях малого числа наблюдений, возможные подходы к прогнозированию коротких временных рядов с привлечением экспертной информации, методы выбора наиболее адекватных моделей. Материал главы содержит изложение новейших достижений в данной области и служит дополнением к главе 5, посвященной статистическому анализу временных рядов. Изложение основано на результатах монографии [9]. 8.1. Понятие короткого временного ряда. Методы описания коротких временных рядов. Проблемы, связанные с анализом и прогнозированием по коротким временным рядам Рассмотрим временной ряд До сих пор (см. главы 5, 6), рассматривая статистические методы оценивания параметров моделей временных рядов и их прогнозирования, мы предполагали, что последовательность наблюдений ряда достаточно велика для того, чтобы проявились асимптотические свойства оценок, то есть получаемые оценки были достаточно близки к их истинным теоретическим значениям. Кроме того, величина периода основания прогноза должна быть достаточной, чтобы можно было на основе прошлых наблюдений выявить тенденции в изменениях значений ряда и провести их прогноз на будущее. Однако, если количество наблюдений n мало (короткий период основания прогноза), удовлетворительный прогноз ряда на основе только прошлых его наблюдений оказывается невозможным и в этом случае требуется привлечение дополнительной информации о прогнозируемом явлении. Формализация понятия "короткий временной ряд" Определим оценку минимального количества наблюдений, при котором можно считать ряд коротким. Рассмотрим модель ряда, систематическая часть которого представляет собой линейный тренд:
где
где t принимает значения из периода упреждения, то есть t = n + 1, n + 2,...,n + m. Применяя метод наименьших квадратов, можно получить оценки параметров модели (8.1) по наблюдениям ряда на периоде основания прогноза
Дисперсии и взаимная ковариация оценок равны
Используя выражения (8.2) - (8.5), определим дисперсию
прогноза
Далее, поскольку
можно записать
Подставим в (8.6) ранее выведенные соотношения (8.3) - (8.5) для дисперсий и ковариации и окончательно получим где
Коэффициент
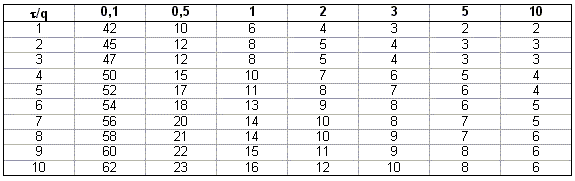
В таблице 8.1 приведены значения Временной ряд
будем называть коротким для заданных m
и q, если период его наблюдений Замечание Выше мы рассмотрели модель
линейного тренда. Аналогично величину
Проблемы, связанные с прогнозированием по коротким временным рядам Основные проблемы, которые возникают при прогнозировании по коротким временным рядам, связаны с недостатком априорной (прошлой) информации о поведении ряда и заключаются в следующем: 1) имея короткий ряд данных невозможно на основе только прошлых наблюдений выявить долгосрочные тенденции развития процесса; 2) оценки параметров модели ряда ненадежны; 3) применение традиционных статистических методов оценки точности прогноза (определение доверительных интервалов, проверка гипотез) оказывается невозможным; 4)
теряет смысл детальный
статистический анализ остатков
модели и, следовательно, критерии
адекватности, такие как 5) при анализе коротких рядов не имеет смысла использовать сложные модели для описания трендов, так как их оценивание требует больших выборок, можно ограничиться линейными или квадратичными трендами. Таким образом, анализ и прогнозирование коротких временных рядов практически невозможны без привлечения дополнительной, экспертной информации о предполагаемых свойствах ряда (наблюдаемого явления).
|