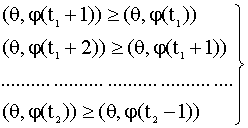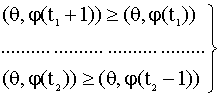8.2. Привлечение экспертной информации при прогнозировании по коротким временным рядам

Эксперт - это специалист в данной предметной области. Он владеет неформальными методами анализа и способен высказывать суждения относительно изучаемого явления, например, о динамике спроса на новые товары или о перспективах развития инновационных технологий. Таким образом, учет мнения эксперта (или нескольких экспертов) в сочетании с формальными (объективными) методами позволяет повысить надежность прогнозов в условиях недостатка наблюдаемых данных. Эксперт может судить о предполагаемых (по его мнению) нижних и верхних границах ("коридоре") значений временного ряда на периоде упреждения прогноза. Он может также высказывать мнение о тенденциях и темпах изменения изучаемого показателя, то есть будет показатель расти или уменьшаться и насколько быстро и т.д. и т.п.

Приведем примеры типичных экспертных суждений.

В дальнейшем именно такого типа высказывания экспертов и будут учитываться при прогнозировании.

Представление суждений в виде неравенств

Будем предполагать, что значения временного ряда на периоде упреждения соответствуют линейной по параметрам аддитивной модели тренда, которую в общем виде можно записать так

(8.8)

где - известные нелинейные функции времени, - параметры модели. Введем векторную функцию и вектор параметров . Используя понятие скалярного произведения векторов (см. приложение), уравнение (8.8) можно записать в виде

(8.9)

где - скалярное произведение векторов и . Прогноз значений ряда определяется с использованием уравнения

(8.10)

Всякое отдельное высказывание эксперта типа 1) - 7) означает, что на параметры модели (8.10) накладываются линейные ограничения вида

(8.11)

где моменты периода упреждения и , а также числовые величины задаются экспертами (их значения соответствуют суждению экспертов).

Рассмотрим, например, высказывание 1). Это высказывание можно представить в виде следующего неравенства

Более сложному высказыванию 3) соответствуют два неравенства

которые можно записать так

Высказыванию 4) соответствует система неравенств вида (8.11)

Высказывание 6) означает, что значения временного ряда до момента возрастают, а после этого момента убывают. Это высказывание можно представить в виде следующей системы неравенств:

(8.12)

(8.13)

причем неравенства (8.12) соответствуют возрастанию значений ряда до момента , а неравенства (8.13) - убыванию ряда после этого момента. Аналогично, можно представить противоположные суждениям 1), 4), 6) высказывания 2), 5), 7).

Задание

Запишите в виде неравенств высказывания экспертов 2), 5), 7).

Если имеется множество экспертных суждений, то их совокупности можно сопоставить систему неравенств вида

которую иначе можно записать так

(8.14)

Совокупность экспертных суждений может включать высказывания разных экспертов, причем отдельный эксперт может представить несколько высказываний, но в любом случае им можно сопоставить систему неравенств вида (8.14).

Непротиворечивость суждений

Совокупность экспертных суждений, представленных системой неравенств (8.14) назовем непротиворечивой, если существует вектор параметров такой, что система неравенств (8.14) совместна.

В противном случае экспертные суждения будем называть противоречивыми.

Пример 8.1

Пусть тренд описывается линейной функцией

Для этой функции экспертные суждения: "значение временного ряда в момент периода упреждения окажется в интервале " и "значение временного ряда в момент периода упреждения окажется в интервале " будут непротиворечивы, если, например, и . Если , то эти высказывания экспертов будут всегда непротиворечивы.

---

назад

предыдущая глава

начало главы

оглавление

следующая глава

вперед

---

Томский государственный университет - 2003