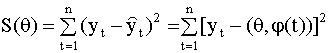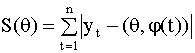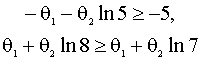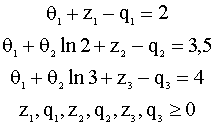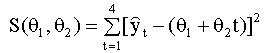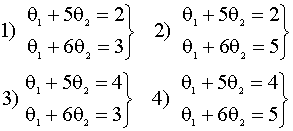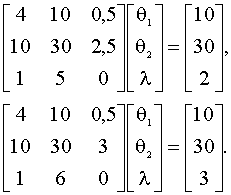Эконометрика

Глава 8. АНАЛИЗ И ПРОГНОЗИРОВАНИЕ КОРОТКИХ ВРЕМЕННЫХ РЯДОВ С ПРИВЛЕЧЕНИЕМ ЭКСПЕРТНОЙ ИНФОРМАЦИИ

8.3. Методы прогнозирования при непротиворечивых экспертных суждениях

Если экспертные суждения непротиворечивы, то система неравенств (8.14) совместна и оценки параметров трендовой модели (8.10) будут удовлетворять одновременно всем неравенствам системы (8.14). В общем случае существует не единственный вектор параметров , удовлетворяющий неравенствам (8.14), то есть система неравенств имеет не единственное решение. Но кроме суждений экспертов (эксперта) в распоряжении аналитика имеются данные наблюдений ряда на периоде основания прогноза. Естественно привлечь эти наблюдения для определения единственного, наилучшего в некотором смысле, согласованного со всеми высказываниями экспертов, решения. Таким образом, задача оценивания параметров модели сводится к задаче оптимизации по критерию наилучшего приближения наблюдаемых данных при ограничениях, соответствующих экспертным суждениям.

8.3.1. Оценивание параметров как решение задачи квадратичного программирования

Выберем в качестве меры близости наблюдаемых и оцененных значений ряда на периоде основания прогноза сумму квадратов остатков модели

(8.15)

Тогда задача оценивания вектора параметров модели формулируется следующим образом: необходимо минимизировать квадратичный критерий (8.15) по вектору при ограничениях

(8.16)

Данная задача относится к классу задач квадратичного программирования и при условии непротиворечивости экспертных суждений, имеет единственное решение. Решение оптимизационной задачи (8.15), (8.16) можно получить только численно. Существуют эффективные численные методы решения подобных задач (они изучаются в курсе "Исследование операций"), которые реализованы во многих пакетах программ, в том числе в Excel.

После того, как оценки параметров получены, строим прогнозную последовательность

(8.17)

где - вектор оценок параметров.

8.3.2. Оценивание параметров как решение задачи линейного программирования

Более простой для численного решения является задача линейного программирования. В связи с этим, сформулируем задачу оценивания параметров трендовой модели в виде задачи линейного программирования. В качестве меры близости наблюдаемых и оцененных значений ряда на периоде основания прогноза возьмем сумму модулей (абсолютных величин) остатков модели

(8.18)

Таким образом, необходимо минимизировать функцию (8.18) при ограничениях (8.16). Функция (8.18) не является линейной, однако сформулированную задачу можно свести к задаче линейного программирования, используя следующий прием. Введем вспомогательные переменные

Нетрудно видеть, что имеют место равенства

(8.19)

(8.20)

Учитывая равенства (8.19), (8.20), задачу минимизации критерия (8.18) при ограничениях (8.16) можно сформулировать в виде следующей эквивалентной задачи линейного программирования: минимизировать линейную функцию

(8.21)

по вектору параметров и переменным при ограничениях (8.16) и дополнительных ограничениях на вспомогательные переменные

(8.22)

(8.23)

Решая задачу линейного программирования (8.21) - (8.23), (8.16), находим вектор оценок параметров .

Таким образом, процедура прогнозирования временного ряда состоит из следующих шагов.

1) На основе экспертных суждений составляем систему линейных ограничений (8.16), которым должны удовлетворять параметры модели тренда.

2) Решаем задачу линейного программирования (8.21) - (8.23), (8.16), определяем вектор оценок параметров модели.

3) Строим последовательность прогнозных значений временного ряда, используя уравнение (8.17).

Замечание

Численное решение задачи линейного программирования существенно проще, чем задачи квадратичного программирования. Для ее решения можно использовать эффективные методы, например, широко известный симплексный метод (он изучается в курсе "Исследование операций"), который реализован во многих пакетах прикладных программ.

Пример 8.2

Пусть известны наблюдения временного ряда: 2; 3,5; 4. На основе содержательного анализа изучаемого явления установлен вид функции тренда

(8.24)

Два эксперта высказали суждения: "значение временного ряда в момент t = 5 периода упреждения окажется не больше 5" и "значение временного ряда в момент периода упреждения окажется не менее, чем в момент ". В данном примере n = 3, k = 2, , , L=2, , , , .

Выполним прогнозирование ряда на периоде упреждения длительностью m = 5 с учетом экспертных суждений.

1) Представим экспертные суждения в виде системы неравенств

Второе неравенство можно переписать в виде

или, замечая, что , имеем .

2) Составим задачу линейного программирования: минимизировать функцию

при ограничениях, составленных на первом шаге и дополнительных ограничениях вида

Решая эту задачу, находим значения оценок , .

3) Строим прогнозную последовательность, используя уравнение (8.24). Получаем; ; ; ; .

8.3.3. Частный случай: прогнозирование по двухпараметрической трендовой модели

В практических приложениях часто бывает достаточно использовать для прогноза относительно простые модели тренда. Рассмотрим одну из таких моделей, которую можно построить без применения аппарата квадратичного программирования.

Пусть модель описывается уравнением

(8.25)

где функция монотонно убывает или монотонно возрастает. Будем учитывать только экспертные суждения интервального типа: "значение временного ряда в момент периода упреждения будет находиться в интервале ", l=1, 2,…,L. Кроме того, будем считать, что два различных суждения не могут относиться к одному и тому же моменту времени, то есть , если . Параметры определим из условия минимума квадратичного критерия

(8.26)

с учетом ограничений, накладываемых в соответствии с суждениями экспертов. Суждения экспертов интервального типа задаются линейными неравенствами вида

(8.27)

(8.28)

Данная задача относится к классу задач квадратичного программирования, однако, оказывается, ее можно решить без привлечения сложных численных алгоритмов.

Учет одного экспертного суждения

Рассмотрим сначала простой случай, когда учитывается только одно экспертное суждение. Поскольку функция (8.26) строго выпукла, решение единственно и находится либо внутри области (полосы)

(8.29)

допустимых решений , либо на одной из ограничивающих эту область прямых:

(8.30)

(8.31)

Учитывая это, для определения оптимального решения можно поступить следующим образом. Сначала минимизировать функцию (8.26) без учета ограничений (8.29). Если полученное решение удовлетворяет неравенствам (8.27), (8.28) (или (8.29)), что можно проверить простой подстановкой, то это и будет оптимальное решение. Если полученное решение не принадлежит области (8.29), то необходимо решить задачу минимизации функции (8.26) с учетом ограничения в виде равенства (8.30), и ту же задачу, но с учетом ограничения в виде равенства (8.31). Из полученных таким образом решений достаточно выбрать то, при котором значение функции (8.26) минимально. Первая задача, по - существу, сводится к обычной задаче оценивания параметров парной линейной регрессии вида (8.25) по методу наименьших квадратов, где в качестве регрессора используется функция .

Задача минимизации функции (8.26) при ограничении в виде равенства (8.30) (или (8.31)) относится к классу задач на условный экстремум (в нашем случае - условный минимум). Ее решение можно получить, используя метод множителей Лагранжа. Получим решение с учетом ограничения (8.30). Составим функцию Лагранжа

где - множитель Лагранжа. Необходимые (а в нашем случае и достаточные) условия минимума функции (8.26) при ограничении (8.30) имеют вид

Дифференцируя функцию Лагранжа по неизвестным параметрам и приравнивая результат к нулю, получаем следующую систему линейных уравнений:

(8.32)

Решая систему (8.32), получаем оценки параметров и при ограничении (8.30). Аналогично, применяя метод множителей Лагранжа, определяем оценки параметров при ограничении (8.31). Далее, подставляя полученные решения в критерий ( 8.26), выбираем то, при котором функция (8.26) будет меньше. Это и будут искомые оценки параметров тренда с учетом экспертного суждения.

Учет нескольких экспертных суждений

Предположим теперь, что имеется несколько непротиворечивых экспертных суждений интервального типа, которым соответствует система неравенств

(8.33)

Область допустимых значений параметров, соответствующая каждому суждению, ограничена двумя прямыми на параметрической плоскости

(8.34)

(8.35)

Пересечение областей вида (8.33) представляет собой выпуклое множество M с границами в виде отрезков прямых. Это множество является выпуклым многоугольником, вершины которого обозначим , где , - индексное множество вершин. Поскольку минимизируемая функция (8.26) строго выпукла, можно показать, что если минимум функции (8.26) не достигается внутри многоугольника, то он достигается в единственной точке на одной из двух сторон многоугольника, примыкающих к вершине, в которой значение функции (8.26) минимально на множестве вершин I. Разумеется, минимум может достигаться и в самой вершине.

Учитывая приведенные выше соображения, можно предложить следующую многошаговую процедуру решения задачи оценивания параметров модели (8.25).

1) Находится решение задачи оценивания по методу наименьших квадратов без учета ограничений. Если полученное решение удовлетворяет всем ограничениям задачи (это проверяется его подстановкой в неравенства (8.33)), то оптимальные оценки найдены, и процедура поиска решения на этом заканчивается.

2) Если окажется, что найденное на первом шаге решение не удовлетворяет хотя бы одному из ограничений (8.33), то находятся вершины многоугольника путем решения четверок систем линейных уравнений вида

(8.36)

и проверки принадлежности каждого решения многоугольнику M (проверка осуществляется подстановкой решений в неравенства (8.33)).

3) Вычисляются значения функции (8.26) в найденных вершинах многоугольника и находится вершина , в которой значение функции минимально. Обозначим и индексы системы уравнений вида (8.36), из решения которой находится точка .

4) Поскольку минимум функции может достигаться либо в найденной на предыдущем шаге вершине многоугольника , либо на одной из примыкающей к ней сторон, необходимо найти еще два решения задачи: минимизировать функцию (8.26) при ограничении в виде равенства

и минимизировать функцию (8.26) при ограничении

где , - правые части уравнений системы, из решения которой найдена вершина . Решение данных задач получаем, применяя метод множителей Лагранжа. Обозначим эти решения и соответственно.

5) Проверяем, принадлежат ли найденные на предыдущем шаге решения многоугольнику M, подставляя их в неравенства (8.33).

6) Среди полученных решений, , , принадлежащих многоугольнику M, выбираем то, при котором функция (8.26) будет минимальна. Это и будет искомой оценкой вектора параметров тренда (8.25).

7) Используя уравнение (8.25), строим прогнозную последовательность , t=n+1,n+2,…,n+m.

Пример 8.3.

Пусть получены следующие наблюдения временного ряда: 1, 2, 3, 4. Модель тренда имеет вид

(8.37)

Имеются два экспертных суждения: "значение временного ряда в момент t = 5 периода упреждения окажется в интервале [2, 4]", "значение временного ряда в момент t = 6 периода упреждения окажется в интервале [3, 5]". Таким образом, в данном случае n=4, k=2, , , L=2, , , , , , .

Необходимо построить прогноз ряда на периоде упреждения m = 5 с использованием модели тренда (8.37), данных наблюдений и экспертных суждений.

В соответствии с описанной выше процедурой выполняем следующие шаги.

1) Находим минимум функции

(8.38)

В результате получаем оценки , ( здесь и далее для простоты истинные значения параметров и их оценки будем обозначать одинаковыми символами). Так как при найденных значениях параметров величины , не принадлежат интервалам и соответственно, переходим к следующему шагу.

2) Находим вершины многоугольника, соответствующего ограничениям, накладываемым экспертными суждениями. Для этого решаем четыре системы линейных уравнений

Находим точки , , , . Нетрудно убедиться, что эти точки принадлежат множеству M и действительно являются вершинами многоугольника (в данном случае это будет параллелограмм, образованный пересечением двух областей, соответствующих экспертным суждениям).

3) Вычисляем значения функции (8.38) в найденных вершинах многоугольника. Получаем , , , . Минимальное значение функции достигается в точке .

4) Точка (вершина многоугольника) находится из решения первой системы уравнений , следовательно, , , , , , . Решаем задачи минимизации функции (8.38) при ограничении, задаваемом первым уравнением системы 1), а затем ту же задачу при ограничении, задаваемом вторым уравнением системы 1). Для этого составляем две системы линейных уравнений вида (8.32)

5) Проверяем, принадлежат ли найденные точки и многоугольнику M, подставляя их в неравенства вида (8.33) при l=1,2. Имеем , , следовательно, неравенства выполняются и точка принадлежит допустимой области решений. Аналогично проверяем второе решение. Для него имеем и , и , следовательно, неравенства также выполняются.